Quaternion Operations

 During our recent diversion into imaginary time, we saw that using the imaginary unit to indicate time can simplify our efforts to express spacetime, but we hit the natural problem in that this benefit vanishes when we tried to introduce more than one spatial dimension.  What if, however, we flipped it?  When discussing the geometric meaning of the metric tensor, we noted that we don't need to use a negative time signature, we can also use a negative space signature.  Can we use imaginary space and still have three spatial dimensions?  

Covariance, Contravariance, and the Metric

  When we discussed the metric before, in the context of deriving the Lorentz Group, it served to generalize the concept of the dot product into four-dimensions.  We've just discussed it in the context of other vector and matrix products as well.  Which should be leading naturally to the question of what other function metric tensors might serve.  To do so we must introduce a key feature of tensor algebra that has been notably absent thus far, the notion of covariant and contravariant tensors.

Relativistic Electromagnetism

We've looked at how forces can be described in relativistic mechanics, but not yet discussed how the fields producing them change.  It's time to correct that oversight by examining the quintessential physics scenario.  

No, not the harmonic oscillator, the other one, the case of a charged particle in an electromagnetic field.

Plot of particle trajectories in EM fields

Let us imagine an electron moving at some relativistic velocity through a combination of electric and magnetic fields.  We need a way to express the fields in both our, laboratory, frame of reference and in the electron's frame.

A Brief Diversion Into Imaginary Time

In our previous entry in our introduction to special relativity, we introduced the interval, or proper time, which provides a four-dimensional extension of length:

 And we noticed the oddity that this extension of squared length seems to have a negative term.

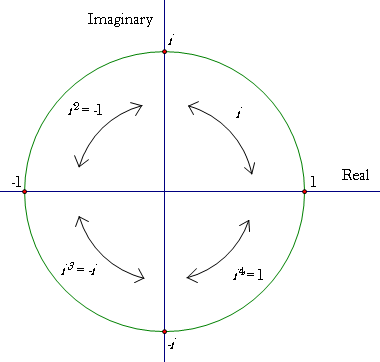
Of course, there is a way that squaring some element can give us a negative number, if time is an imaginary quantity.  Let's consider the case of one spatial dimension.  A general vector representing a separation between two events, Δ, with one time and one space component, might be written as:

This has some convenience, since it clearly separates space from time within the term in a manner similar to basis vectors.  We can express events using the complex plane, where the imaginary axis becomes the temporal axis and the real axis a spatial axis.

As discussed before, a boost can be viewed as a rotation in 4 dimensions.  Rotations in the complex plane can be described according to Euler's formula:

A rotation by the angle, ϕ, is a multiplication by this unit norm complex number.

   We therefore need only find a way to relate this unusual spacetime angle to velocity.  Keep in mind that if time is imaginary then so must be the time derivative:

 Remember that the tangent is the derivative dx/dτ: 

 So we can find the angle, with one tiny wrinkle, that imaginary unit.  When that appears, we need to invoke hyperbolic trig functions to move it outside the function:

Thanks to similar relationships, we can rewrite our sine and cosine terms above using their hyperbolic equivalents as below, where we'll make the substitution ϕ → iϕ to simplify our expression:

And thanks to some basic properties of hyperbolic trig functions:

 Demonstrating that we can quite easily rewrite our earlier matrix representation of the boost using this new angle we've introduced, which is termed the rapidity.  This is equivalent to the boost matrix from before:

 Rapidity is often useful as it allows for adding velocities easily.  Two successive boosts can be represented using the same formalism as:

  So rapidity has utility outside the niche application of imaginary time.  We can move between complex and matrix representations of a two dimensional system by the comparison:

And from this we'll finally express the Lorentz Boost in 2d using a purely complex representation:

 Plotting the complex rotation term we see that both the real (cosh) and imaginary (sinh) components explode as rapidity approaches ±10.  Note also that, plotting β in terms of rapidity, we'll see that it asymptotically approaches 1 well before rapidity reaches 10:

  The imaginary time formalism isn't very popular as it does not provide much in the way of insight beyond more traditional four-vectors.  And you know what's better than using an obscure formalism to derive a useful tool?  Jumping from it into an entirely new formalism!  After all, space isn't one dimensional, it's three dimensional.  To generalize complex spacetime, let's find a 3+1d representation.  Fortunately, exactly such a number system exists, quaternions.  Can we find a quaternion formalism that effectively describes special relativity?  Let's see.

Universal Speeding: The Lorentz Group

 There are two important, well-known rules about interstellar travel:

1.  Nothing can travel faster than light.
2.  If you want to get anywhere interesting in a reasonable amount of time then you need to go faster than light.

This leads to three options:

1.  You just can't go anywhere. 
2.  You can go someplace nearby, but you have to stay on your ship for a very long time. 
3.  You must break rule one.

Option 1 can be rejected as boring.  Option 2 I've already looked at in the form of generation ships.  Let's talk about Option 3: If the speed of light is the universal speed limit then let's start speeding.  Before we can exceed the speed limit we need to know what the speed limit is, and why it's the limit.  So why can't anyone go faster than the speed of light?  Let's have a look.

Let's begin with some very basic concepts in Special Relativity, because we'll need them later.  Typically this is introduced in introductory classes at the university and high school level by arbitrarily introducing something called the Lorentz Factor, γ.  A better introduction might show how γ can be derived from Galilean Relativity and Lorentz Invariance as we did in the previous post.

While this approach is useful and instructive for discussing ideas like time dilation and length contraction, and while it does demonstrate why we shouldn't be able to exceed the speed of light, it doesn't help us understand the source of these issues much less suggest a way to solve them.  

To do that, we'll need to introduce the formal language of four-vectors to discuss in detail how time and space are connected.