The Starship Engineer's Notebook: Quaternion Operations

During our recent diversion into imaginary time, we saw that using the imaginary unit to indicate time can simplify our efforts to express spacetime, but we hit the natural problem in that this benefit vanishes when we tried to introduce more than one spatial dimension. What if, however, we flipped it? When discussing the geometric meaning of the metric tensor, we noted that we don't need to use a negative time signature, we can also use a negative space signature. Can we use imaginary space and still have three spatial dimensions?

As it happens, there is a four-dimensional extension of complex numbers: Quaternions, first discovered by Irish physicist and mathematician William Rowan Hamilton in 1843. Hamilton found that he could expand a single imaginary dimension into three:

$\begin{align}i^2=j^2=k^2&=ijk=-1\\ij=-ji&=k\\jk=-kj&=i\\ki=-ik&=j\end{align}$

Hamilton divided his quaternions into two parts: the scalar, or "real" component; and the vector, or "imaginary" components:

$\underline{q}=q_0+\vec{q}=q_0+q_1i+q_2j+q_3k$

Hamilton was responsible for introducing the term "vector" to physics and for the popular i, j, k notation used in 3d vectors. However, quaternion mechanics largely fell by the wayside by the end of the 19th century, in favor of 3d vector notation.

Quaternion Operations

One huge advantage of quaternions is that multiplication subsumes both dot and cross products from conventional, 3d mechanics, along with scalar multiplication. Expressing the multiplication of two quaternions, a and b, using vector product notation:

$(\underline{a})(\underline{b})=(a_0b_0-\vec{a}\cdot\vec{b})+(a_0\vec{b}+b_0\vec{a}+\vec{a}\times\vec{b})$

Note that if there is no zero (scalar) component to the quaternions a and b, meaning that they have only vector components, what Hamilton called "pure quaternions," then we have just the two vector products. The presence of scalar components adds additional terms to the product. We should also immediately see that multiplication is not commutative, since the cross product is anti-commutative:

$\underline{ba}=(a_0b_0-\vec{a}\cdot\vec{b})+(a_0\vec{b}+b_0\vec{a}-\vec{a}\times\vec{b})$

The magnitude of a complex number is square root of the number multiplied by its conjugate the same is true of a quaternion. As we have chosen to represent quaternions with underlining, let's express their conjugate with an overline. By analogy with complex numbers, we'll find:

$\begin{align}|z|^2=z\cdot z^*&\rightarrow|\underline{a}|^2=\underline{a}\overline{a}\\z^*=x-yi&\rightarrow\overline{a}=a_0-\vec{a}\end{align}$

Which, by applying the above rules for multiplication, yields a scalar value, as we should expect:

$|{a}|^2=\underline{a}\bar{a}=a_0^2+|\vec{a}|^2$

Rearranging the magnitude, we can find the inverse of a quaternion in terms of the conjugate and magnitude:

$\begin{align}(\underline{a})(\underline{a})^{-1}&=1\\\rightarrow(\underline{a})^{-1}&=\frac{\bar{a}}{a^2}\end{align}$

All of this is very simply derived from the core rules outlined above. It will be helpful later on to consider the case where some quaternion, b, from the left and right by a and its conjugate:

$\underline{a}\underline{b}\bar{a}=a_0^2(b_0+\vec{b})+|\vec{a}|^2(b_0-\vec{b})+2a_0\vec{a}\times\vec{b}+2(\vec{a}\cdot\vec{b})\vec{a}$

Quaternion Commutators and Anti-Commutators

We can separate the product into commutative and anti-commutative parts. The commutator [a,b] shows us the anti-commuting part, because it is zero if a and b commute. The anti-commutator {a,b} = 0 if a and b anti-commute and shows the commuting part of of the product. The product of two quaternions can be expressed as the sum (or difference) of the commutator and anti-commutator:

$\begin{align}\{\underline{a},\underline{b}\}&=\frac{1}{2}(\underline{ab}+\underline{ba})=\left(a_0b_0-\vec{a}\cdot\vec{b}\right)+\left(a_0\vec{b}+b_0\vec{a}\right)\\\left[\underline{a},\underline{b}\right]&=\frac{1}{2}\left(\underline{ab}-\underline{ba}\right)=\vec{a}\times\vec{b}\\\underline{ab}&=\{\underline{a},\underline{b}\}+\left[\underline{a},\underline{b}\right]\\\underline{ba}&=\{\underline{a},\underline{b}\}-\left[\underline{a},\underline{b}\right]\end{align}$

Let's consider the product of three quaternions cab in terms of the commutator and anti-commutator:

$\begin{align}\{\underline{c},[\underline{a},\underline{b}]\}=\{[\underline{a},\underline{b}],\underline{c}\}&=-\vec{c}\cdot(\vec{a}\times\vec{b})+c_0(\vec{a}\times\vec{b})\\\left[\underline{c},\{\underline{a},\underline{b}\}\right]=-[\{\underline{a},\underline{b}\},\underline{c}]&=a_0(\vec{c}\times\vec{b})+b_0(\vec{c}\times\vec{a})\\\left[\underline{c},[\underline{a},\underline{b}]\right]=-[[\underline{a},\underline{b}],\underline{c}]&=\vec{c}\times(\vec{a}\times\vec{b})=(\vec{b}\cdot\vec{c})\vec{a}-(\vec{a}\cdot\vec{c})\vec{b}\\\{\underline{c},\{\underline{a},\underline{b}\}\}=\{\{\underline{a},\underline{b}\},\underline{c}\}&=c_0(a_0b_0-\vec{a}\cdot\vec{b})-(a_0\vec{b}\cdot\vec{c}+b_0\vec{a}\cdot\vec{c})+c_0(a_0\vec{b}+b_0\vec{a})+\vec{c}(a_0b_0-\vec{a}\cdot\vec{b})\\\underline{cab}&=[\underline{c},[\underline{a},\underline{b}]]+\{\underline{c},\{\underline{a},\underline{b}\}\}+[\underline{c},\{\underline{a},\underline{b}\}]+\{\underline{c},[\underline{a},\underline{b}]\}\end{align}$

It's helpful to look at multiplication using the commutator and anti-commutator, as there are situations where some of these terms will go towards zero. As it will happen, later we'll want to consider the situation where a = c and:

$\begin{align}\{\underline{a},[\underline{a},\underline{b}]\}&=\left[\underline{a},\{\underline{a},\underline{b}\}\right]=a_0(\vec{a}\times\vec{b})\\\left[\underline{a},\left[\underline{a},\underline{b}\right]\right]&=|\vec{a}|^2\vec{b}-(\vec{b}\cdot\vec{a})\vec{a}\\\{\underline{a},\{\underline{a},\underline{b}\}\}&=a_0^2b_0-2a_0(\vec{a}\cdot\vec{b})-b_0|\vec{a}|^2+a_0^2\vec{b}+2a_0b_0\vec{a}-(\vec{a}\cdot\vec{b})\vec{a}\end{align}$

Quaternion Calculus

The differential operator can be represented as a quaternion:

$\begin{align}\nabla=\frac{\delta}{\delta_0}+i\frac{\delta}{\delta_1}+j\frac{\delta}{\delta_2}+k\frac{\delta}{\delta_3}\end{align}$

So, if we want to express some quaternionic derivative:

$\begin{align}\nabla\underline{b}&=\{\nabla,b\}+\left[\nabla,b\right]\\\{\nabla,\underline{b}\}&=\left(\delta_0 b_0-\vec{\nabla}\cdot\vec{b}\right)+\left(\delta_0\vec{b}+\vec{\nabla}b_0\right)\\&=\delta_0b_0-\delta_1b_1-\delta_2b_2-\delta_3b_3+i(\delta_0b_1+\delta_1b_0)+j(\delta_0b_2+\delta_2b_0)+k(\delta_0b_3+\delta_3b_0)\\\left[\nabla,\underline{b}\right]&=\vec{\nabla}\times\vec{b}\\&=i(\delta_2b_3-\delta_3b_2)+j(\delta_3b_1-\delta_1b_3)+k(\delta_1b_2-\delta_2b_1)\end{align}$

Which, we notice subsumes both the concept of the divergence and curl, as we should expect. The double derivative is then, and we immediately get to apply the above multiplication (cab) rule above:

$\begin{align}\{\underline{\nabla},\{\underline{\nabla},\underline{b}\}\}&=\left(\delta_0^2b_0-2\delta_0\vec{\nabla}\cdot\vec{b}-\vec{\nabla}^2b_0\right)+\left(\delta_0^2\vec{b}+2\delta_0\vec{\nabla}b_0-\vec{\nabla}(\vec{\nabla}\cdot\vec{b})\right)\\\left[\underline{\nabla},\left[\underline{\nabla},\underline{b}\right]\right]&=\vec{\nabla}\times(\vec{\nabla}\times\vec{b})=\vec{\nabla}(\vec{\nabla}\cdot\vec{b})-\vec{\nabla}^2\vec{b}\\\{\underline{\nabla},[\underline{\nabla},\underline{b}]\}&=[\underline{\nabla},\{\underline{\nabla},\underline{b}\}]=\delta_0(\vec{\nabla}\times\vec{b})\end{align}$

Where we again see familiar vector calculus terms like the vector Laplacian appear. Note the difference between the two double vector derivatives:

$\begin{align}\vec{\nabla}^2\vec{b}&=i\nabla^2b_1+j\nabla^2b_2+k\nabla^2b_3\\&=i(\delta_x^2+\delta_y^2+\delta_z^2)b_x+j(\delta_x^2+\delta_y^2+\delta_z^2)b_y+k(\delta_x^2+\delta_y^2+\delta_z^2)b_z\\\vec{\nabla}\left(\vec{\nabla}\cdot\vec{b}\right)&=\vec{\nabla}\left(\delta_1b_1+\delta_2b_2+\delta_3b_3\right)\\&=i\delta_x(\delta_xb_x+\delta_yb_y+\delta_zb_z)+j\delta_y(\delta_xb_x+\delta_yb_y+\delta_zb_z)+k\delta_z(\delta_xb_x+\delta_yb_y+\delta_zb_z)\end{align}$

And, naturally, we quickly see how the complete double-differential can be found by putting these terms together. Putting everything together, we get the double derivative:

$\begin{align}\underline{\nabla\nabla b}=\left(\delta_0^2 b_0-2\delta_0\vec{\nabla}\cdot\vec{b}-\vec{\nabla}^2 b_0\right)+\left(\delta_0^2\vec{b}+2\delta_0\vec{\nabla}b_0-\vec{\nabla}^2\vec{b}+2\delta_0\vec{\nabla}\times\vec{b}\right)\\\bar{\nabla}\bar{\nabla}\underline{b}=\left(\delta_0^2 b_0+2\delta_0\vec{\nabla}\cdot\vec{b}-\vec{\nabla}^2 b_0\right)+\left(\delta_0^2\vec{b}-2\delta_0\vec{\nabla}b_0-\vec{\nabla}^2\vec{b}-2\delta_0\vec{\nabla}\times\vec{b}\right)\end{align}$

It can also be easily shown that:

$\nabla^2\underline{b}=\underline{\nabla}\bar{\nabla}\underline{b}=\bar{\nabla}\underline{\nabla}\underline{b}=\left(\delta_0^2+\vec{\nabla}^2\right)\left(b_0+\vec{b}\right)$

Quaternions As Rotations

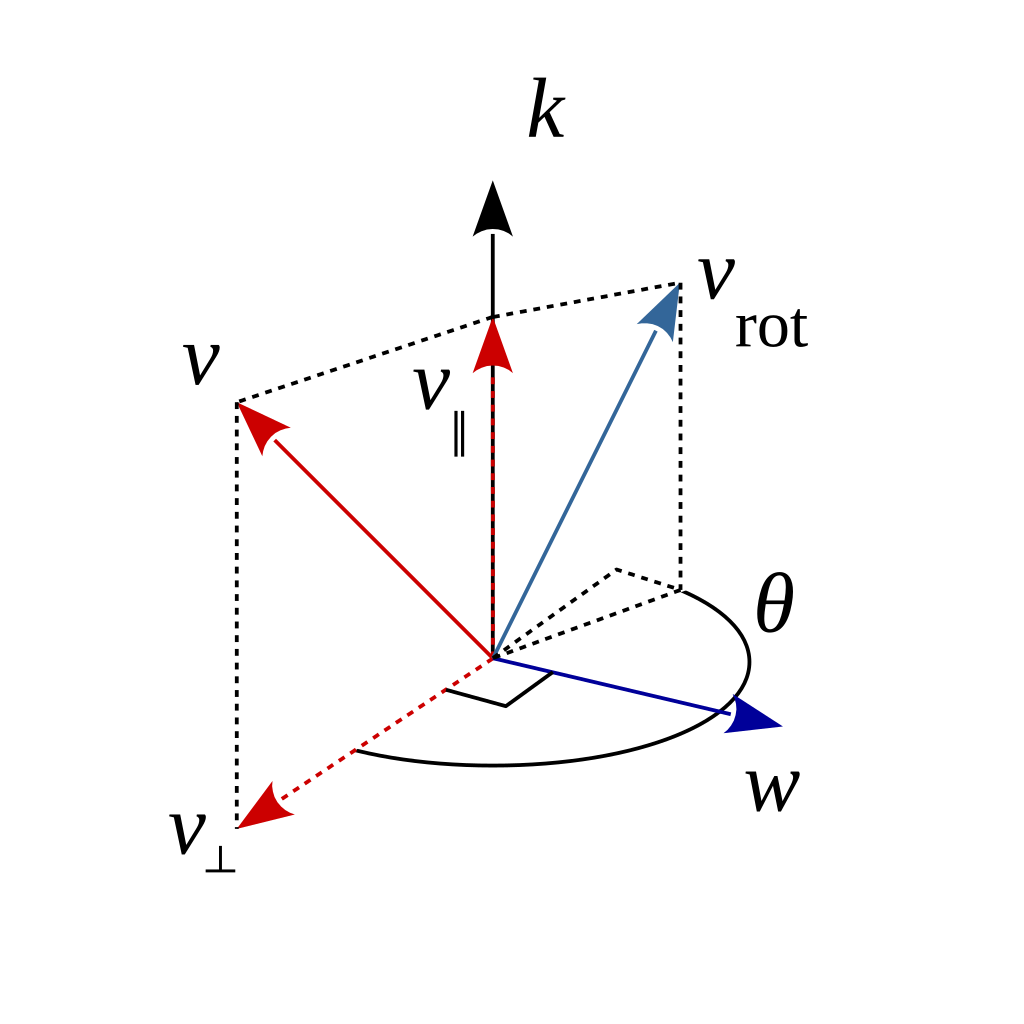
Rather than using 3x3 matrices to represent rotations in three dimensional space, we can use quaternions for that task. To describe the rotation of some vector v around an axis, k, by some angle, θ:

$\begin{align}\vec{v}_\parallel&=\vec{k}\cdot\vec{v}\\\vec{v}_\perp&=\vec{v}-\vec{v}_\parallel\\\vec{v}_{rot\parallel}&=\vec{v}_\parallel=\vec{k}\cdot\vec{v}\\\vec{v}_{rot\perp}&=\cos(\theta)\vec{v}_\perp+\sin(\theta)\vec{v}\\\vec{v}_{rot}&=\vec{v}_{rot\perp}+\vec{v}_{rot\parallel}\end{align}$

Let's look at this problem in a purely vector viewpoint, before considering quaternions. If we project v onto the axis, that is we take the dot product of v and k, we get the parallel component of the vector. The perpendicular component is just the difference between v and the parallel component. We know the parallel component won't change on a rotation about the axis and the perpendicular component is rotated in a plane perpendicular to the rotation axis as shown above.

Putting the two components back together:

$\begin{align}\vec{v}_{rot}&=\vec{v}_{rot\perp}+\vec{v}_{rot\parallel}=\cos(\theta)\vec{v}+\left(\vec{k}\times\vec{v}\right)\sin(\theta)+\left(1-\cos(\theta)\right)\left(\vec{k}\cdot\vec{v}\right)\vec{k}\end{align}$

This looks like what we got when we multiplied some quaternion, b, from either side by some other quaternion and its conjugate. Define two pure quaternions, v and q:

$\begin{align}\underline{v}{'}&=0+\vec{v}_{rot}\\&=\underline{q}\underline{v}(q)^{-1}=\underline{q}\underline{v}\bar{q}\\\underline{v}&=0+\vec{v}\\\underline{q}&=\cos\left(\frac{\theta}{2}\right)+\vec{k}\sin\left(\frac{\theta}{2}\right)\end{align}$

Since k is defined as a unit vector, q is a unit quaternion. This has proven to be one of the most popular modern applications of quaternions, as quaternion rotations don't suffer the sort ambiguities that can arise from traditional Euler angles and rotation matrices.

Two successive rotations can simply be described by multiplying the quaternions together as:

$\begin{align}\underline{q}&=\underline{q}_1\underline{q}_2\\\underline{q}^{-1}&=\bar{q}=\bar{q}_2\bar{q}_1\end{align}$

Note that, generally speaking, for two vectors the typical scalar multiplication rule does not apply:

$\exp(\vec{u}_1)\exp(\vec{u}_2)\neq\exp(\vec{u}_1+\vec{u}_2)$

We can do this only if the two quaternions commute, which happens if the two vectors are linearly dependent.

Quaternions As Exponential Functions

It's trivial to convert from polar to Cartesian coordinates, which makes it equally simple to make such a transition in complex number systems. To represent a 2d polar system using complex numbers we know from Euler's forumula:

$z=x+iy=r\left(\cos(\theta)+i\sin(\theta)\right)=re^{i\theta}$

Where the radial distance in the complex plane, r, is the magnitude of the complex number, z. Extending the idea of polar decomposition into quaternion space suggests:

$\begin{align}\underline{a}&=a_0+\vec{a}=|\underline{a}|\left(\frac{a_0}{|\underline{a}|}+\frac{\vec{a}}{|\vec{a}|}\frac{|\vec{a}|}{|\underline{a}|}\right)\\&=|\underline{a}|\left(\cos(\varphi)+\hat{a}\sin(\varphi)\right)\\&=|\underline{a}|\exp{\hat{a}\varphi}\end{align}$

The newly introduced angle, φ, is some direction in 4 dimensional space which distinguishes the scalar axis from the vector axes, just as θ did in the 2d complex plane. The unit vector, represented by the ^ term above, extends the function of i in the complex plane into quaternionic space. It's easy to see that the conjugate of a is a transformation of φ → -φ:

$\bar{a}=|\underline{a}|(\cos(\varphi)-\hat{a}\sin(\varphi))$

We can, in turn, represent the unit vector in spherical coordinates:

$\hat{u}=i\cos(\theta)+j\sin(\theta)\cos(\psi)+k\sin(\theta)\sin(\psi)$

The exponential representation gives us a simple method for taking the exponent of a quaternion:

$\underline{q}^{x}=|\underline{q}|^{x}\exp(\hat{u}\varphi)^{x}=|\underline{q}|^{x}\exp(\hat{u}x\varphi)=|\underline{q}|^{x}\left(\cos(x\varphi)+\hat{u}\sin(x\varphi)\right)$

Four Dimensional Rotations As Quaternion Pairs

It should be clear, given the similarities between these two descriptions that the quaternion method of describing 3d rotations can be considered a special case of rotation in 4d, where the plane of rotation always includes the scalar axis. There are three vector axes perpendicular to the scalar axis, leading to three possible planes of rotation. There are three remaining planes, which allow rotations of the scalar portion and leave two vector axes unchanged. These, together with the other three rotation planes, for a rotation of some vector v by an angle θ:

$\begin{matrix}R^\theta_{1x}(v)=e^{-i\theta/2}(v)e^{i\theta/2}&R^\theta_{yz}(v)=e^{i\theta/2}(v)e^{i\theta/2}\\R^\theta_{1y}(v)=e^{-j\theta/2}(v)e^{j\theta/2}&R^\theta_{xz}(v)=e^{j\theta/2}(v)e^{j\theta/2}\\R^\theta_{1z}(v)=e^{-k\theta/2}(v)e^{k\theta/2}&R^\theta_{xy}(v)=e^{k\theta/2}(v)e^{k\theta/2}\\\end{matrix}$

For a basic 3d rotation, the left and right rotations are conjugates but for some general 4d double-rotation they need not have any particular relationship. Double rotations, with two independent planes of rotation, become possible in 4 or more dimensions.

In 2d, there is only the plane of rotation and the rotation takes place around a single point that does not move. In 3d, there is a line, the axis of rotation, that is left unchanged. In 4 dimensions an entire plane is left independent of the rotation, allowing for a second, completely independent rotation to take place. Double rotations in four dimensions again leave a single point unchanged.

4d isoclinic rotation of a tesseract

A special case where the two rotation angles have the same magnitude is termed an isoclinic rotation. If the rotation angles are equal, it is termed a left isoclinic rotation and if they are opposite, a right isoclinic rotation. The spatial rotation is a special case where the two axes are also the same and with opposite angles. In this case, the two planes of rotation are orthogonal, for example a rotation in the (x,y) plane and a simultaneous rotation in the (1,z) plane.

Any four dimensional rotation can be expressed as a pair of isoclinic rotations.

Imagine a double-rotation composed of a simultaneous rotation by θ in the {1,x} plane and by ϕ in the {y,z} plane. The four dimensional rotation matrix can be described, in block notation:

$R=\begin{bmatrix}\Theta&0\\0&\Phi\end{bmatrix}$

where the two square sub-matrices:

$\begin{matrix}\Theta=\begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{bmatrix}&\Phi=\begin{bmatrix}\cos\phi&-\sin\phi\\\sin\phi&\cos\phi\end{bmatrix}\end{matrix}$

Define two new angles:

$\begin{align}\alpha&=\tfrac{1}{2}(\theta+\phi)\\\beta&=\tfrac{1}{2}(\theta-\phi)\end{align}$

From these definitions, we can rewrite the rotation matrix as the product of two isoclinic rotations:

$R=M_L M_R$

where the left and right isoclinic rotation matrices are:

$\begin{matrix}M_L=\begin{bmatrix}\cos\alpha&-\sin\alpha&0&0\\\sin\alpha&\cos\alpha&0&0\\0&0&\cos\alpha&-\sin\alpha\\0&0&\sin\alpha&\cos\alpha\end{bmatrix}&M_R=\begin{bmatrix}\cos\beta&-\sin\beta&0&0\\\sin\beta&\cos\beta&0&0\\0&0&\cos(-\beta)&-\sin(-\beta)\\0&0&\sin(-\beta)&\cos(-\beta)\end{bmatrix}\end{matrix}$

Performing this rotation R upon some four dimensional vector Q is equivalent to multiplying some quaternion q from the left and right:

$\begin{align}Q'=RQ&=M_L M_R Q=M_R M_L Q\\\leftrightarrow\underline{q}'&=\underline{z}_L\underline{q}\underline{z}_R\end{align}$

Working out both sets of multiplication, with the components of Q and q equated, allows us to solve for the components of the left and right quaternions:

$\begin{align}\underline{z}_L=\cos(\alpha)+i\sin(\alpha)=\exp(i\alpha)\\\underline{z}_R=\cos(\beta)+i\sin(\beta)=\exp(i\beta)\end{align}$

For some double-rotation taking place in two orthogonal planes {a,b} and {b,c} we can write the same rotation matrix within the {a,b,c,d} coordinate system and convert back to the standard {1,i,j,k} system:

$\begin{align}R_{1ijk}&=S^{-1}R_{abcd}S=\left(S^{-1}_L M_L S_L\right)\left(S^{-1}_R M_R S_R\right)\\&\Rightarrow\begin{matrix}M_{L;1ijk}=S^{-1}_L M_{L;ab,cd}S_L\\M_{R;1ijk}=S^{-1}_R M_{R;ab,cd}S_R\end{matrix}\end{align}$

Generally, 4d rotation matrices can be converted into quaternions per:

$\begin{align}\underline{z}_L=a+bi+cj+dk\leftrightarrow M_L=\begin{bmatrix}a&-b&-c&-d\\b&a&-d&c\\c&d&a&-b\\d&-c&b&a\end{bmatrix}\\\underline{z}_R=a+bi+cj+dk\leftrightarrow M_R=\begin{bmatrix}a&-b&-c&-d\\b&a&d&-c\\c&-d&a&b\\d&c&-b&a\end{bmatrix}\end{align}$

The Starship Engineer's Notebook

Dropdown Navigation

May 14, 2025

Quaternion Operations

Quaternion Operations

Quaternion Commutators and Anti-Commutators

Quaternion Calculus

Quaternions As Rotations

Quaternions As Exponential Functions

Four Dimensional Rotations As Quaternion Pairs

Any four dimensional rotation can be expressed as a pair of isoclinic rotations.

No comments:

Post a Comment