Habitability of Binary and Trinary Star Systems

For a story he's working on my father asked me what sunrise and sunset would look like on a planet with three suns.  The question seemed to warrant investigation.

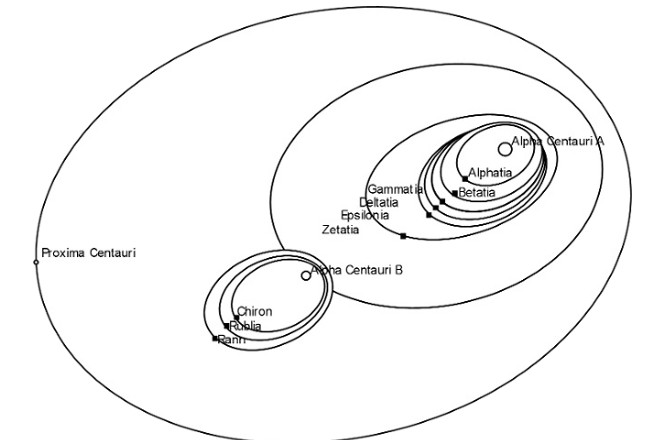
Naturally we have to start with what, exactly, multiple star systems look like.  Consider the Alpha Centauri system:

Note two stars Alpha Centauri A and B in orbit around each other with a third star, Proxima Centauri orbiting the binary system.  Normally the three body problem has no closed form solution, it cannot by analytically solved but can only be investigated by simulation.  However this system can be approximated as a collection of two body problems.  One with the primary and secondary star orbiting each other about their center of mass, and another with the ternary star and the binary pair in orbit about each other.  In this case the first problem involves solving a two body problem with A and B, and the second involves another two body problem with the combined set of A and B and Proxima.
It can also be seen from the image above that both Alpha Centauri A and B can support planetary systems.  The question here is could a multiple star system support a life bearing planet?

First consider where the planet orbits the system.  In a binary system a planet could conceivably orbit either member, provided there is adequate separation between the two that it is allowed to form at all.  The planet could also, however, orbit the center of mass of the binary system.  Rather than orbiting either star it orbits both stars, with a focus at their center of mass and with a total mass equal to the sum of their masses.  Could such a planet support life?
Neglecting more complex analysis the rule of thumb for the center of a star's habitation zone in astronomical units is based on the luminosity, L, of the sun in terms of stellar luminosities:
 
Note that Earth is actually inside the center of the sun's habitability zone by 0.34AU.  The zone is large enough to also encompass Mars, which is too small to maintain a dense atmosphere and has no appreciable magnetic field to protect it from solar radiation.  It is thought that only stars of stellar class F, G, K, and M can support life.  Larger stars are too short-lived to allow life bearing planets to evolve.
For a planet orbiting both members of a binary system we would use their combined luminosity.  If the two stars are extremely close together then this is the only way they can support planets at all, tidal forces between them would destroy a body in orbit about one or the other.  In such a tightly orbiting system one or both stars may be larger than their Roche lobe.  This typically invisible line determines the range of dominance by one body in a two-body system.  Material inside a star's Roche lobe is bound to that star.  If the star's radius is larger than its Roche lobe then some stellar material is actually bound to its partner, forming an accretion disk abound the heavier body.  If both stars are larger than their Roche lobes then they begin to merge, stellar material moving freely from one body to the other.  Such a condition can lead to the two stars fully merging into one.  The boundary of the Roche lobe for one member, where a is the semimajor axis of the system and q is the ratio of their masses m1/m2:

What do we get from this?  For a planet to orbit two suns, and those two suns to visibly be such, they must orbit with a semimajor axis (a=a1+a2, the system semimajor axis equals the sum of the individual semimajor axes) greater than some value based on their masses and radii.  In turn the planet must be some distance from the pair, this distance substantially larger than the distance between the two stars.  Dividing the habitability distance by the separation of the two stars:

The constant portion and that depending on q, the mass ratio, approaches 87.5 as the ratio nears 0 and 233 as it nears infinity (for a mass ratio of one it gives 108).  We can simplify our criterion to one based only on the sum of luminosities and the radius of the larger star, in terms of solar luminosity and radius (the selection of 1 is arbitrary, it simply places the above criterion at somewhere between 87.5 and 233):

This isn't a difficult criterion to use nor is it that strict.  However these conditions, extremely tight stellar orbits, are less common than more distantly orbiting stars.
For a planet to orbit only one star it must be inside that star's Roche lobe, which must in turn extend beyond the star's own habitability zone.  Not only must the planet be within the habitability zone of its parent (the star which it orbits) but it must also not be exposed to unnecessarily harsh conditions from the partner star, nor should it suffer too severe changes during its revolution.  Excepting, again, the second Lagrange point, the orbit of the planet will put it between the two stars at one point in its orbit and facing them both at the opposite point.
Consider first the requirement, that of the orbit.  We'll take another look at the Roche lobe, last time we found the minimum separation based on stellar radius.  This time we'll find the limit of the star's reach from the separation.  Require that the Roche lobe extend beyond the habitation zone.  Using the same limits found above we have an equation dependent only on the binary system's semimajor axis and the parent star's luminosity.  The limit as q approaches zero is 0.3 and as it approaches infinity is 0.82.  For a mass ratio of 1 this term is 0.38.

This requirement is even easier than the above one to meet.  The left hand size is unlikely to exceed about 3 for a large F type star.  This requires at most a stellar separation of only 10 AU's.
Although this ensures the planet is bound to its parent star and at an appropriate range from it, it does not address the added problem of light from the companion star.  In this case the concern is the intensity of stellar radiation from the stars.  Intensity is simply the luminosity of the star divided by the surface area of a sphere at the radius we are considering from the center.  So the total intensity reaching the planet is the contribution from both stars.  When one side is facing both stars the intensity is:

(Note that when using astronomical units we can ignore the 4-pi terms, doing so will give us the intensity in terms of the average intensity of sunlight reaching earth)
At the opposite end of its orbit one side of the planet is facing either sun.  So there is a different, but not negligible, intensity hitting both the day and night sides of the planet

For life to evolve and prosper on this planet the intensity must be in a tolerable range during both seasons, without a severe shift between them.  This can easily happen for a very low L2 or high a.
If we treat the planet as a black body then we can still add the intensities, even when facing different sides of the planet.  Planets are not, of course, generally black bodies.  Earth's greenhouse layer prevents it from radiating heat at that rate.  However any system with heat input and output, even Venus which has an extremely thick greenhouse layer, achieves an equilibrium temperature.  Heat in should equal heat out for any system.  So the temperature in terms of intensity, emissivity (for earth about 0.64) and albedo (earth's 0.3):

The rate of heat input is, naturally, proportional to the intensity of incident light.  Simply multiply the value of I by heat reaching earth from the sun (S=1367 W/m2).  If the difference in intensity is small then the difference in temperature will be too.  We've already seen what the minimum possible allowable spacing is, it's the case where rough a=3r.  Using that and solving, with representative values for earth, for distance is astronomical units and luminosity in stellar luminosities provided the change in T is significantly smaller than T:

Of course it isn't necessarily that simple.  Not only have we neglected axial tilt, we've also forgotten that the greenhouse layer can suffocate a planet.  Using the example of Venus again, if surface temperature gets too high the greenhouse layer thickens due to evaporation, increasing heat retention and further increasing surface temperature.  For high surface temperatures the emissivity is a function of temperature.  If, however, these two temperatures are kept within an acceptable range then this won't become a problem.  And so another criteria, for any habitable planet really, becomes its emissivity, or the thickness of its greenhouse layer.
So now we have a planet in the appropriate butter zone.  It's just far enough away from the suns not to fry or be torn apart by tidal forces, close enough to get enough light and heat for life to form.  It doesn't experience too extreme a temperature difference between seasons or between night and day.  These are, naturally, not the only requirements, but other constraints are similar to those on planets orbiting a single star system.

A third star in the system can be approximated like the Alpha Centauri system shown above.  Primary and secondary companions orbit each other and this binary system is itself in orbit with a ternary companion.  This makes an ordinarily unsolvable three body problem into a solvable two body problem.  Doing so also greatly simplifies our question of the habitability of this system.  If the planet orbits the ternary member then we can simply reuse our previous analysis exactly, save that now the second star becomes the sum of the binary pair.  The solution for intensity, surface temperature, and temperature difference is unchanged.  Distances involved will be much greater, so much so that we can simplify somewhat:

But chances are that the separation, a, between the ternary and binary pair will be so great that the second term will be negligible.
This holds exactly if the planet orbits the binary pair, the only difference is which term is divided by r and which by a:

If the planet orbits one member of the binary pair the influence of the ternary is the same.  Distance between planet and ternary is great enough that the planet's location in its orbit does not seriously impact the intensity of light it receives.  So the temperature increases slightly, but the difference in temperature between seasons remains the same.

Finally we have one last concern.  So far we've assumed circular orbits for simplicity.  But binary orbits are not generally circular.  For a planet orbiting a safe distance away from a binary pair this makes no difference.  However if the planet is orbiting one star in a binary or trinary system then the difference in temperature due to eccentricity is likely to be much higher than the difference from facing.

The eccentricity dependent part of this equation is nearly linear in the 0 - 1 range.  eccentricity cannot actually equal 1 for a stable orbit, e=1 gives an escape trajectory.  At the largest value, e=1, this term is about 0.3.  Combine that with reasonable terrestrial albedo and emissivity values.  Given the luminosity of the the range of stars we're considering the fourth root of luminosity is in a range of about 0.5 to 1.5, most being very close to 1.  So the temperature difference is about:

Which gives us a range of allowable eccentricities and semi-major axes for the binary pair.


What we've found here is that life can indeed develop in a multiple star system provided the basic requirements are met.  For a planet revolving about a binary pair it requires only that the pair be closely orbiting and that the planet be an adequate distance from the pair.  If the planet orbits one member of a pair we add the requirement that the difference in temperature caused by presence or absence of the companion star not be extreme.  For a trinary system we can use the same kind of method, simply treating the binary as one body when it interacts with its ternary member.  Indeed one could have two binary systems interacting in this method the create a 4 star system, and so on to model even larger systems.